Meine kleine Sammlung an Börsenstatistiken (Seite 19)
eröffnet am 02.08.17 21:51:33 von
neuester Beitrag 03.01.24 14:57:17 von
neuester Beitrag 03.01.24 14:57:17 von
Beiträge: 204
ID: 1.258.587
ID: 1.258.587
Aufrufe heute: 38
Gesamt: 23.631
Gesamt: 23.631
Aktive User: 0
ISIN: US78378X1072 · WKN: CG3AA5
5.065,04
PKT
+0,19 %
+9,80 PKT
Letzter Kurs 17.04.24 Citigroup
Neuigkeiten
07:36 Uhr · wallstreetONLINE Redaktion |
22:19 Uhr · dpa-AFX |
20:11 Uhr · dpa-AFX |
19:19 Uhr · Markus Fugmann Anzeige |
16:52 Uhr · dpa-AFX |
Beitrag zu dieser Diskussion schreiben
Sharpe Ratio Wikifolios (1)
Hier ist mir ein Wikifolio namens "CDAX-Werte Alpha" aufgefallen mit ausgesprochen hohem Sharpe Ratio von z.Z. 1.70:https://www.wikifolio.com/de/de/w/wfalfacdax
(wie woanders bereits erwähnt, alles über 1.0 langfristig ist börsengenie-mässig und auch Glück. Langfrsitig hier wieder mit 15Y und mehr definiert.)
=> der grosse Knackpunkt: Wikifolio erklärt nicht, wie genau das Sharpe Ratio bei Ihnen berechnet wird, v.a. nicht über Anlagezeiträume von mehreren Jahren hinweg. Zumindest konnte ich dazu bisher nichts finden.
=> die Wahrscheinlichkeit, dass obiges Sharpe Ratio "in Wahrheit" viel zu hoch ist, ist sehr gross.
Hier ist ein sehr guter Warnhinweis, dass Sharpe Ratios teilweise extremen Schwankungen unterliegen können, wenn der (historische) Betrachtungszeitraum unangemessen kurz ist (der Artikel erwähnt das auch indirekt im vorletzten Satz):
http://www.frasee-investors.com/2013/05/was-ist-ein-sharpe-r…
=> das Wikifolio "VP Defensiv" https://www.wikifolio.com/de/de/w/wf000vp001 wurde seinerzeit noch mit einem extrem hohen Wert von 3.1 beworben:

__
(obige Seite weist Defizite bzgl. ihrer Aussagen zum Sharpe Ratio auf; das soll aber nicht das Thema hier sein. Es sind typische, aber ungenaue und unvollständige Aussagen zum Sharpe Ratio.)
...nur um heute, 25.8.2017 und 4 Jahre später, auf nur noch 0.41 zusammengefallen zu sein:

Antwort auf Beitrag Nr.: 55.466.658 von faultcode am 05.08.17 23:16:12
(a)
Ich will hier kein Fass über MR auchmachen (es bleibt von oben noch genug zu tun), aber mir ist ein MM-Artikel 2017/08 (*) über den heissen Reifen der Berenberg Privatbank (BPB) seit 2010 untergekommen.
Hier füllt eine kleine dt. Privatbank Lücken im dt. und europäischen Kapitalmarkt, die die grossen wie Dt.Bank, Commerzbank etc. seit 2009 zunehmend bewusst liegengelassen haben:
=> mittlerweile liegt die Eigenkapitalrendite bei nahezu 100% (2016):
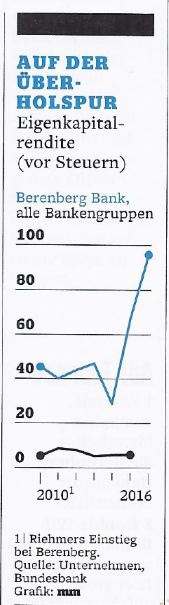
Wenn man nun annimmt - zu oben, dass der USA-Aktienmarkt sich im Bereich ein Tops befindet, dann könnte man auch annehmen, dass die Party der BPB als Power House bei europ. Small- und Midcaps auch irgendwann in 2018...2020(?) vorbei sein könnte.
Ich ahne daher Schlimmes für Evotec und Co. in mittlerer Zukunft. Aber solange diese Party, unterstützt von immer neuen Analysen der BPB ("Die Privatbank Berenberg hat das Kursziel für Evotec nach starken Quartalsergebnissen von 13 auf 16 Euro angehoben."" (***) ), anhält, wird halt dazu getanzt. (Also (teil-)verkaufen sie ihre Evotec-Anteile noch nicht!)
Man sollte allerdings wissen, wann die Party allmählich vorbei ist.
D.h., wann in den USA die QE- und andere geldpolitische Zügel wieder angezogen werden - und damit der Treibstoff für den jetzigen Aktienboom mit viel superbilligem Geld gedrosselt wird.
Auch eine kleine Drosselung kann schon den ein oder anderen Margin call auslösen, und damit eine Kettenrekation.
Man könnte aber auch die immer noch wachsende Privat-Kreditblase in China zum Anlass nehmen (o).
Man kann sich dann den eigentlichen Anlass zur 15...25%-Korrektur - nicht Crash!/FC (im Nachhinein) aussuchen.
Und dann spielt es keine Rolle, ob sich Deutschland dann noch in einem Auftrags- und Beschäftigungsboom befindet oder nicht.
Mich erinnert das an die Zeit des Zweiten Golfkrieges 1991, an die sich in den USA eine Rezession anschloss, die mitten in den westdeutschen Wiedervereinigungsboom hineinkrachte - und dieser damit auch vorerst vorbei war:
- einige dt. Aktiendickschiffe haben sich davon erst wieder bis Ende der 90er Jahre erholt (Mannesmann z.B.):
So könnte es auch vielen der (noch) von der BPB bejubelten Aktienstars gehen.
(Die Aktenanalysen der BPB sind auch nicht besser als die der früheren, grossen dt. "Investmentbanken": die Annahmen ihrer DCF-Kalkulationen liegen im Dunkeln für Aussenstehende:
=> ist wie Leberkäs: schmeckt gut; man will aber lieber nicht wissen, was drinnen ist und wie er gemacht wurde.)
Dass Hendrik Riehmer offenbar beruflich eine "Rampensau"/MM ist, macht die Sache umso bedenklicher. Er wird nicht der Verlierer sein, wenn es zur MR bei der Eigenkapitalrendite der BPB kommt. Bis dahin hat er nämlich schon viel/genug Geld verdient. (Aber ich nicht...)
Lt. MM erwartet er, Hendrik Riehmer, selber "den Crash im Herbst 2019" - vielleicht sollten das die Marktteilnehmer, die auf die BPB-Analysen jetzt noch hören, wissen.
(b) zur Handelsstrategie des Staffeltraders (+) und die sichtbare Divergenz:
Auch nach mehreren Strategiewechsel, die ich nicht mehr genau im Kopf habe, ist doch klar, dass dem dort vorgestellten Handel (bewusst oder unbewusst) eine klassische MR-Strategie zugrunde liegt (++).
Ich schätze Staffeltrader und seine Beträge sehr. Und nun, nach vergangener Handelswoche, zeichnet sich wohl ab, dass diese MR-Handelsstrategie nicht (mehr) funktioniert.
Systematisch kommen 2017 gemischte, aber abgestürzte SP500-Werte nicht wieder in einem erwarteten Zeitraum zurück nach oben - und der Trader wird ungewollt zum Investor.
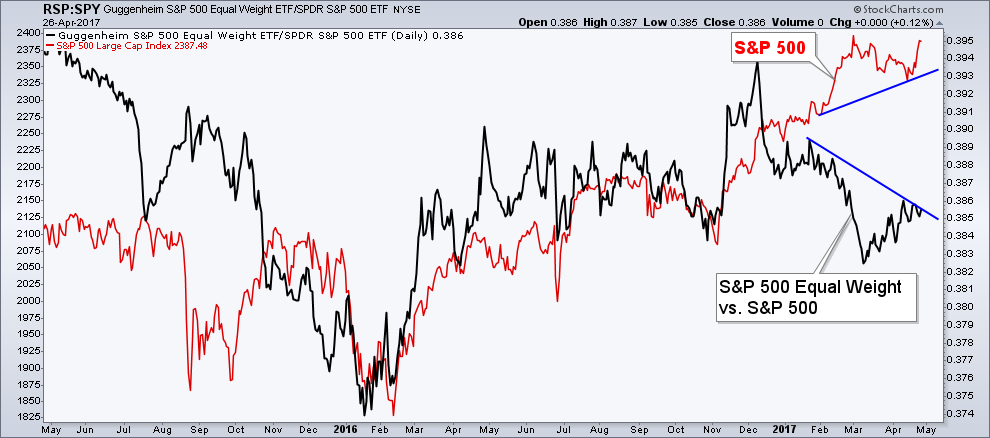
Für mich ist das eine ernstzunehmende Divergenz, und sich charttechnisch wie mehrfach in Beitrag Nr. 8 bereits auch erwähnt, so darstellt (+++) --> kein gutes Zeichen im Allgemeinen (u):
__
(*) http://www.manager-magazin.de/unternehmen/banken/berenberg-h…
(**) aus: https://en.wikipedia.org/wiki/Mean_reversion_(finance)
--> siehe auch: https://en.wikipedia.org/wiki/Regression_toward_the_mean
(***) z.B.:
https://www.wallstreet-online.de/nachricht/9830463-berenberg…
https://www.wallstreet-online.de/nachricht/9827703-berenberg…
(+) https://www.wallstreet-online.de/diskussion/1249084-161-170/…
(++) https://www.quantopian.com/posts/enhancing-short-term-mean-r…
(+++) https://finance.yahoo.com/news/a-growing-divergence-in-perfo…
(o) https://www.wallstreet-online.de/diskussion/1218056-1351-136…
(u) diese Schere kann natürlich auch wieder geschlossen werden. Aber auch so ein Öffnen - Schliessen - Öffnen - Schliessen... ist mMn ein Zeichen eines (breiten) Tops.
Zwischeneinwurf: Boom am Top? Eigenkapitalrendite der Berenberg Bank und drohende Mean Reversion
(mean reversion (MR) is the assumption that a stock's price will tend to move to the average price over time (**) - hin zum langjährigen, positiven "Drift"/FC)(a)
Ich will hier kein Fass über MR auchmachen (es bleibt von oben noch genug zu tun), aber mir ist ein MM-Artikel 2017/08 (*) über den heissen Reifen der Berenberg Privatbank (BPB) seit 2010 untergekommen.
Hier füllt eine kleine dt. Privatbank Lücken im dt. und europäischen Kapitalmarkt, die die grossen wie Dt.Bank, Commerzbank etc. seit 2009 zunehmend bewusst liegengelassen haben:
=> mittlerweile liegt die Eigenkapitalrendite bei nahezu 100% (2016):

Wenn man nun annimmt - zu oben, dass der USA-Aktienmarkt sich im Bereich ein Tops befindet, dann könnte man auch annehmen, dass die Party der BPB als Power House bei europ. Small- und Midcaps auch irgendwann in 2018...2020(?) vorbei sein könnte.
Ich ahne daher Schlimmes für Evotec und Co. in mittlerer Zukunft. Aber solange diese Party, unterstützt von immer neuen Analysen der BPB ("Die Privatbank Berenberg hat das Kursziel für Evotec nach starken Quartalsergebnissen von 13 auf 16 Euro angehoben."" (***) ), anhält, wird halt dazu getanzt. (Also (teil-)verkaufen sie ihre Evotec-Anteile noch nicht!)
Man sollte allerdings wissen, wann die Party allmählich vorbei ist.
D.h., wann in den USA die QE- und andere geldpolitische Zügel wieder angezogen werden - und damit der Treibstoff für den jetzigen Aktienboom mit viel superbilligem Geld gedrosselt wird.
Auch eine kleine Drosselung kann schon den ein oder anderen Margin call auslösen, und damit eine Kettenrekation.
Man könnte aber auch die immer noch wachsende Privat-Kreditblase in China zum Anlass nehmen (o).
Man kann sich dann den eigentlichen Anlass zur 15...25%-Korrektur - nicht Crash!/FC (im Nachhinein) aussuchen.
Und dann spielt es keine Rolle, ob sich Deutschland dann noch in einem Auftrags- und Beschäftigungsboom befindet oder nicht.
Mich erinnert das an die Zeit des Zweiten Golfkrieges 1991, an die sich in den USA eine Rezession anschloss, die mitten in den westdeutschen Wiedervereinigungsboom hineinkrachte - und dieser damit auch vorerst vorbei war:
- einige dt. Aktiendickschiffe haben sich davon erst wieder bis Ende der 90er Jahre erholt (Mannesmann z.B.):

So könnte es auch vielen der (noch) von der BPB bejubelten Aktienstars gehen.
(Die Aktenanalysen der BPB sind auch nicht besser als die der früheren, grossen dt. "Investmentbanken": die Annahmen ihrer DCF-Kalkulationen liegen im Dunkeln für Aussenstehende:
=> ist wie Leberkäs: schmeckt gut; man will aber lieber nicht wissen, was drinnen ist und wie er gemacht wurde.)
Dass Hendrik Riehmer offenbar beruflich eine "Rampensau"/MM ist, macht die Sache umso bedenklicher. Er wird nicht der Verlierer sein, wenn es zur MR bei der Eigenkapitalrendite der BPB kommt. Bis dahin hat er nämlich schon viel/genug Geld verdient. (Aber ich nicht...)
Lt. MM erwartet er, Hendrik Riehmer, selber "den Crash im Herbst 2019" - vielleicht sollten das die Marktteilnehmer, die auf die BPB-Analysen jetzt noch hören, wissen.
(b) zur Handelsstrategie des Staffeltraders (+) und die sichtbare Divergenz:
Auch nach mehreren Strategiewechsel, die ich nicht mehr genau im Kopf habe, ist doch klar, dass dem dort vorgestellten Handel (bewusst oder unbewusst) eine klassische MR-Strategie zugrunde liegt (++).
Ich schätze Staffeltrader und seine Beträge sehr. Und nun, nach vergangener Handelswoche, zeichnet sich wohl ab, dass diese MR-Handelsstrategie nicht (mehr) funktioniert.
Systematisch kommen 2017 gemischte, aber abgestürzte SP500-Werte nicht wieder in einem erwarteten Zeitraum zurück nach oben - und der Trader wird ungewollt zum Investor.
Für mich ist das eine ernstzunehmende Divergenz, und sich charttechnisch wie mehrfach in Beitrag Nr. 8 bereits auch erwähnt, so darstellt (+++) --> kein gutes Zeichen im Allgemeinen (u):

__
(*) http://www.manager-magazin.de/unternehmen/banken/berenberg-h…
(**) aus: https://en.wikipedia.org/wiki/Mean_reversion_(finance)
--> siehe auch: https://en.wikipedia.org/wiki/Regression_toward_the_mean
(***) z.B.:
https://www.wallstreet-online.de/nachricht/9830463-berenberg…
https://www.wallstreet-online.de/nachricht/9827703-berenberg…
(+) https://www.wallstreet-online.de/diskussion/1249084-161-170/…
(++) https://www.quantopian.com/posts/enhancing-short-term-mean-r…
(+++) https://finance.yahoo.com/news/a-growing-divergence-in-perfo…
(o) https://www.wallstreet-online.de/diskussion/1218056-1351-136…
(u) diese Schere kann natürlich auch wieder geschlossen werden. Aber auch so ein Öffnen - Schliessen - Öffnen - Schliessen... ist mMn ein Zeichen eines (breiten) Tops.
!
Dieser Beitrag wurde von CloudMOD moderiert. Grund: Löschung auf Wunsch des Users
Antwort auf Beitrag Nr.: 55.476.648 von faultcode am 08.08.17 05:09:16
e^(a*b) = (e^a)^b
=>
exp(µ + 0,5*σ^2) = exp(µ) * exp(0,5*σ^2)) = exp(µ) * exp(σ^2)^0,5 = exp(µ) * SQRT(exp(σ^2))
Calculating returns (5) - Rechnen mit Logarithmus- und Expoentialfunktion (2)
Eine Gleichung bräuchten wir noch (siehe E[X] = exp(µ + 0,5*σ^2) = exp(µ)*SQRT(exp(σ^2)) oben):e^(a*b) = (e^a)^b
=>
exp(µ + 0,5*σ^2) = exp(µ) * exp(0,5*σ^2)) = exp(µ) * exp(σ^2)^0,5 = exp(µ) * SQRT(exp(σ^2))
Antwort auf Beitrag Nr.: 55.476.645 von faultcode am 08.08.17 04:53:10
..mit diesem Diagramm zum besseren Verständnis:
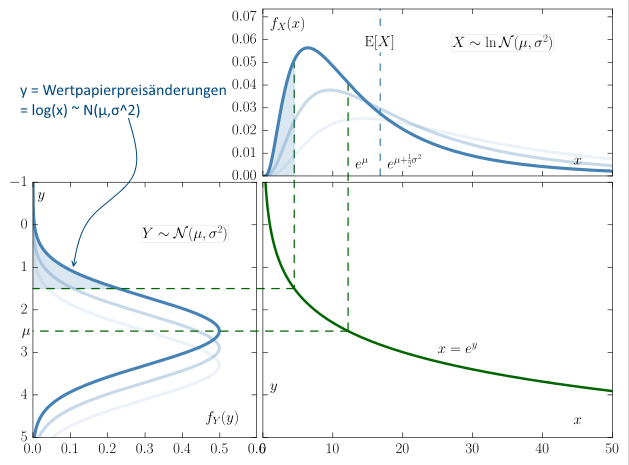
=> hier gilt:
Zufallsvariable Y = µ + σZ
(µ = Mittelwert/mean, σ = Standardabweichung/standard deviation = SQRT(variance) )
mit Z als:
- standard normal deviate or
- standard normal variable or
- standard normal random variable, a normally distributed random variable with expected value µ = 0 and variance σ^2 = 1 (https://en.wikipedia.org/wiki/Standard_normal_deviate)
=> ist nun Y wie oben dargestellt normalverteilt, dann ist X log-normalverteilt: x = exp(y)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
X hat dann diese wichtigen Eigenschaftten:
x ∈ (0, +∞)
Medianwert = Geometrischer Mittelwert GM hier : Med[X] = GM[X] = exp(µ)
arithmetischer Mittelwert (AM)/mean/expected value/Erwartungswert:
E[X] = exp(µ + 0,5*σ^2) = exp(µ)*SQRT(exp(σ^2)) = GM[X]*SQRT(GVar[X])
mit GVar[X] = geometrische Varianz = exp(σ^2)
=> auch hier gilt: GM < AM (weil exp(µ) < exp(µ + 0,5*σ^2) ) --> https://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_g… ("Inequality of arithmetic and geometric means")
Ist logA(Y) normalverteilt, dann ist auch logB(Y) normalverteilt mit A, B ≠ 1 und > 0.
Ist exp(X) log-normalverteilt, dann ist auch A^X log-normalverteilt mit A ≠ 1 und > 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Also, ist Zufallsvariable X log-normalverteilt, dann ist Y = log(X) normalverteilt.
Umgekehrt, ist Y normalverteilt, dann ist X = exp(Y) log-normalverteilt (siehe (e2) aus Beitrag Nr. 16 oben - nur X und Y vertauscht), und nimmt nur positive Werte an:
=> Wertpapier-Preise an der Börse rutschen nicht ins Negative! (wie praktisch )
)
D.h., wie auch für andere, ähnliche Prozesse sind Wertpapier-Preise das multiplikative Produkt von vielen, voneinander unabhängigen Zufallsvariablen, jede davon positiv.
=> also werden zur einfacheren Rechnung alle Wertpapier-Preisänderungen x (zunächst) als log-normalverteilt angenommen - und damit sind alle y = log(1+ri) = log(x), siehe oben, als (zunächst) normalverteilt angenommen. (siehe Beitrag Nr. 14 --> (1) )
Calculating returns (4) - Log returns für die Berechnung der Annual.Vola (2b) - Log-normal distribution
Hier eine wichtige Wikipedia-Seite dazu: https://en.wikipedia.org/wiki/Log-normal_distribution..mit diesem Diagramm zum besseren Verständnis:

=> hier gilt:
Zufallsvariable Y = µ + σZ
(µ = Mittelwert/mean, σ = Standardabweichung/standard deviation = SQRT(variance) )
mit Z als:
- standard normal deviate or
- standard normal variable or
- standard normal random variable, a normally distributed random variable with expected value µ = 0 and variance σ^2 = 1 (https://en.wikipedia.org/wiki/Standard_normal_deviate)
=> ist nun Y wie oben dargestellt normalverteilt, dann ist X log-normalverteilt: x = exp(y)
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
X hat dann diese wichtigen Eigenschaftten:
x ∈ (0, +∞)
Medianwert = Geometrischer Mittelwert GM hier : Med[X] = GM[X] = exp(µ)
arithmetischer Mittelwert (AM)/mean/expected value/Erwartungswert:
E[X] = exp(µ + 0,5*σ^2) = exp(µ)*SQRT(exp(σ^2)) = GM[X]*SQRT(GVar[X])
mit GVar[X] = geometrische Varianz = exp(σ^2)
=> auch hier gilt: GM < AM (weil exp(µ) < exp(µ + 0,5*σ^2) ) --> https://en.wikipedia.org/wiki/Inequality_of_arithmetic_and_g… ("Inequality of arithmetic and geometric means")
Ist logA(Y) normalverteilt, dann ist auch logB(Y) normalverteilt mit A, B ≠ 1 und > 0.
Ist exp(X) log-normalverteilt, dann ist auch A^X log-normalverteilt mit A ≠ 1 und > 0
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Also, ist Zufallsvariable X log-normalverteilt, dann ist Y = log(X) normalverteilt.
Umgekehrt, ist Y normalverteilt, dann ist X = exp(Y) log-normalverteilt (siehe (e2) aus Beitrag Nr. 16 oben - nur X und Y vertauscht), und nimmt nur positive Werte an:
=> Wertpapier-Preise an der Börse rutschen nicht ins Negative! (wie praktisch
 )
)D.h., wie auch für andere, ähnliche Prozesse sind Wertpapier-Preise das multiplikative Produkt von vielen, voneinander unabhängigen Zufallsvariablen, jede davon positiv.
=> also werden zur einfacheren Rechnung alle Wertpapier-Preisänderungen x (zunächst) als log-normalverteilt angenommen - und damit sind alle y = log(1+ri) = log(x), siehe oben, als (zunächst) normalverteilt angenommen. (siehe Beitrag Nr. 14 --> (1) )
Antwort auf Beitrag Nr.: 55.476.645 von faultcode am 08.08.17 04:53:10
https://en.wikipedia.org/wiki/Volatility_(finance)#Crude_vol…
..noch eine grobe Faustformel (die mMn Sinn macht) zur Berechnung der annualisierten Volatilität:
σann_est = 16 x σd (Gl.8a)
mit σd die beobachtete tägliche Änderung bzw. Volatilität eines Wertpapieres (über einen etwas längeren Zeitraum), z.B. +/-1%.
=> σann_est = 16 x 1% = 16%
...weil 16^2 = 256 Handelstage pro Jahr angenommen, was nahe bei h = 250...255 liegt.
__
Den zweiten Absatz in diesem Kapital halte ich für sehr fraglich, da er mit einem Korrektur-Faktor arbeitet, der hier mMn nicht angebracht ist - und die Faustformal-Vola mit 1 / correction factor c4(n=2) = 1/(√(2/π)) beaufschlagen würde, also um 1.2533 erhöhen würde => Vorsicht: eine zu hohe Vola macht Finanzinstrumente uU zu teuer (und die Sharpe Ratio zu niedrig etc.)!
Dieser Faktor kommt von hier: https://en.wikipedia.org/wiki/Unbiased_estimation_of_standar…
=> dort geht es darum, die (wahre) Standardabweichung (bei Normalverteilung) abzuschätzen, wenn nur n = 2, 3, 4,... Stichproben vorliegen, was aber für die Anwendung der Faustformel nicht unbedingt gegeben sein muss. Auch gibt Wikipedia keine Quelle für diese Korrektor an!
(Wenn man es "ziemlich" genau wissen muss/will, dann darf man eh nicht mit Faustformeln arbeiten.)
Calculating returns (4) - Log returns für die Berechnung der Annualisierten Volatilität (2a) - Faustformal
Unter https://en.wikipedia.org/wiki/Volatility_(finance) gibt es bei:https://en.wikipedia.org/wiki/Volatility_(finance)#Crude_vol…
..noch eine grobe Faustformel (die mMn Sinn macht) zur Berechnung der annualisierten Volatilität:
σann_est = 16 x σd (Gl.8a)
mit σd die beobachtete tägliche Änderung bzw. Volatilität eines Wertpapieres (über einen etwas längeren Zeitraum), z.B. +/-1%.
=> σann_est = 16 x 1% = 16%
...weil 16^2 = 256 Handelstage pro Jahr angenommen, was nahe bei h = 250...255 liegt.
__
Den zweiten Absatz in diesem Kapital halte ich für sehr fraglich, da er mit einem Korrektur-Faktor arbeitet, der hier mMn nicht angebracht ist - und die Faustformal-Vola mit 1 / correction factor c4(n=2) = 1/(√(2/π)) beaufschlagen würde, also um 1.2533 erhöhen würde => Vorsicht: eine zu hohe Vola macht Finanzinstrumente uU zu teuer (und die Sharpe Ratio zu niedrig etc.)!
Dieser Faktor kommt von hier: https://en.wikipedia.org/wiki/Unbiased_estimation_of_standar…
=> dort geht es darum, die (wahre) Standardabweichung (bei Normalverteilung) abzuschätzen, wenn nur n = 2, 3, 4,... Stichproben vorliegen, was aber für die Anwendung der Faustformel nicht unbedingt gegeben sein muss. Auch gibt Wikipedia keine Quelle für diese Korrektor an!
(Wenn man es "ziemlich" genau wissen muss/will, dann darf man eh nicht mit Faustformeln arbeiten.)
Antwort auf Beitrag Nr.: 55.476.645 von faultcode am 08.08.17 04:53:10
The Complete Guide to Option Pricing Formulas, Haug, 2nd ed., 2007
http://www.espenhaug.com/books.html
=> über 90% der vorgestellten Formeln basieren auf lognormal distributions:
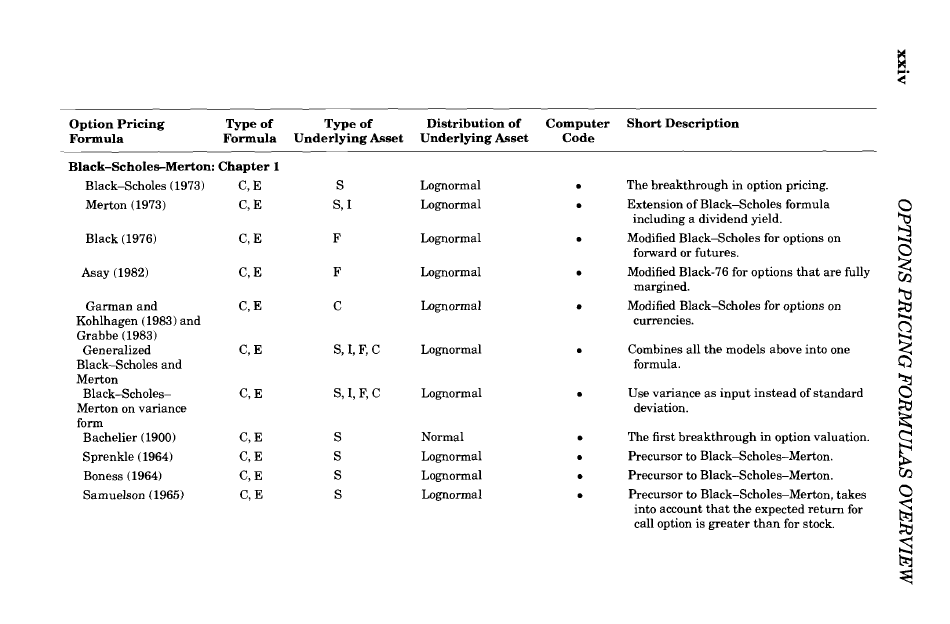
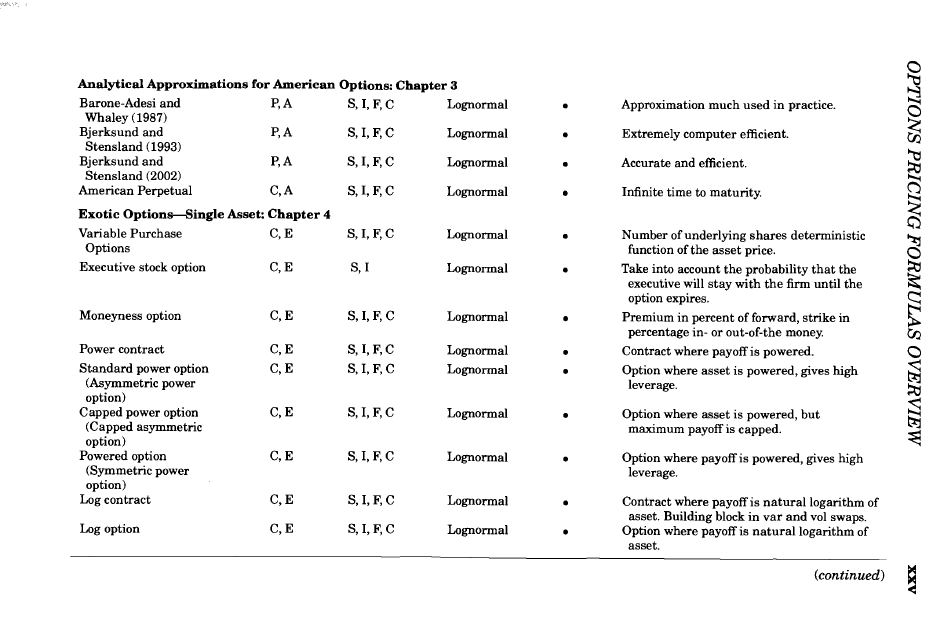
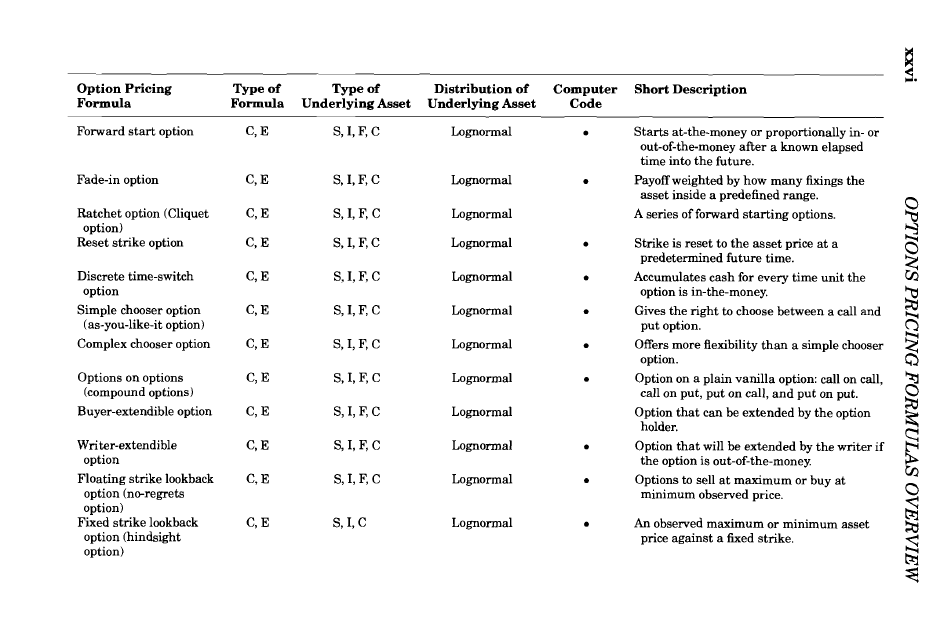
usw....
Calculating returns (6) - Log returns als Basis für die meisten Option pricing formulas
wie hier gesehen:The Complete Guide to Option Pricing Formulas, Haug, 2nd ed., 2007
http://www.espenhaug.com/books.html
=> über 90% der vorgestellten Formeln basieren auf lognormal distributions:



usw....
Antwort auf Beitrag Nr.: 55.476.645 von faultcode am 08.08.17 04:53:10
ln(x · y) = ln(x) + ln(y); x; y > 0
ln(x/y) = ln(x) − ln(y); x; y > 0
ln(x^y) = y ln(x); x > 0
d ln(x)/dx = 1/x ; x > 0
d/dx ln(f (x)) = 1/f(x)· d/dx f(x) (chain-rule)
ln(1) = 0 and ln(x) -> −∞ für x-> 0
---
e^1 = 2.718: that is, ln(x) is defined such that x = ln(e^x)
e^xe^y = e^(x+y)
e^xe^(−y) = e^(x−y)
(e^x)^y = e^(xy)
eln(x) = x
d/dx e^x = e^x
d/dx e^f(x) = e^f(x) d/dx f(x) (chain-rule)
Calculating returns (5) - Rechnen mit Logarithmus- und Expoentialfunktion
Zum Kapitelabschluss noch ein paar Gleichungen zum einfachen Rechnen mit geometrischen Renditen:ln(x · y) = ln(x) + ln(y); x; y > 0
ln(x/y) = ln(x) − ln(y); x; y > 0
ln(x^y) = y ln(x); x > 0
d ln(x)/dx = 1/x ; x > 0
d/dx ln(f (x)) = 1/f(x)· d/dx f(x) (chain-rule)
ln(1) = 0 and ln(x) -> −∞ für x-> 0
---
e^1 = 2.718: that is, ln(x) is defined such that x = ln(e^x)
e^xe^y = e^(x+y)
e^xe^(−y) = e^(x−y)
(e^x)^y = e^(xy)
eln(x) = x
d/dx e^x = e^x
d/dx e^f(x) = e^f(x) d/dx f(x) (chain-rule)
Antwort auf Beitrag Nr.: 55.476.597 von faultcode am 08.08.17 01:13:47
=> diese berechnete (=STABW.S(xx:yy)) Standardabweichung muss idR auf ein Jahr skaliert werden, um Vergleichbarkeit mit Zinssätzen etc. zu ermöglichen.
Da wir wie oben schon angedeutet unsere Log Returns als log-normal, also als normal verteilt annehmen (+), können wir - und nur dann - die Skalierung über diese Beziehung einfach vornehmen (aus (a) in Beitrag Nr. 13 --> ch.2.6 Volatility):
rt = ln(Pt) - ln(P(t-1)) ~ N(μ, σ^2) (Gl.7a)
mit N(μ, σ^2) als Normverteilung mit (wahrem) Mittelwert μ und (wahrer) Varianz = Standardabweichung^2 = σ^2.
Für h > 0, Anzahl der gleichdistanten Beobachtungen in einem Jahr, gilt dann entsprechend:
r(t+h) ~ N(μh, hσ^2) (Gl.7b)
Wenn wir also das erste Formelergebnis zur Standardabweichung σ0 mit dem Faktor √(h) (Wurzel von h) gewichten, bekommen wir die Annualisierte Volatilität:
σann = √(h)σ0 (Gl.8)
Also, bei:
- täglichen Log returns nehmen wir h = 250...255 (ich nehme immer unbesehen 254 - die Anzahl der Handelstage pro Jahr ist weltweit unterschiedlich und am selben Markt durch sich verschiebende Feiertage auch nicht immer konstant über die Jahre hinweg)
- wöchentlichen Log returns nehmen wir h = 52, und bei
- monatlichen Log returns nehmen wir h = 12.
__
Hier ist ein Beispiel dazu aus: http://www.investopedia.com/ask/answers/021015/how-can-you-c…
=>
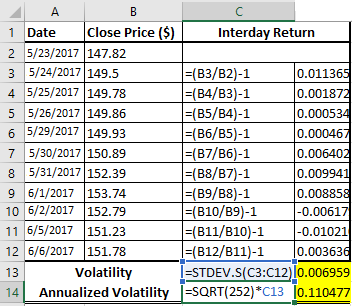
A priori halte ich an dieser Stelle fest:
1. die täglichen Renditen sind hier arithmetisch, nicht logarithmisch. Die arithmetischen Renditen können durchaus als normalverteilt angenommen werden, um zu einem besseren Ergebnis bzgl. der Annualisierten Volatilität zu kommen.
2. diese Annahme ist aber nur implizit durch mich gemacht worden, nicht durch den Autor. Damit kann dieses Beispiel auf einer nicht beabsichtigten Annahme beruhen und damit das Ergebnis verfälschen (bei kleinen Zeiträumen spielt so eine Ergebnis-Verfälschung noch keine grosse Rolle, aber bei Berechnungen über mehrere Jahre hinweg, v.a. bei möglicher zunehmender Volatilität und Abnahme der zeitlichen Aüflösung, also von Tag zu Woche zu Monat usw. --> (e), (f) )
Daher zur Veranschaulichung mein Nachbau mit den arithmetischen (simplen, linearen) Tagesrenditen (rechts) und meinen logarithmischen (geometrischen) Renditen (links):
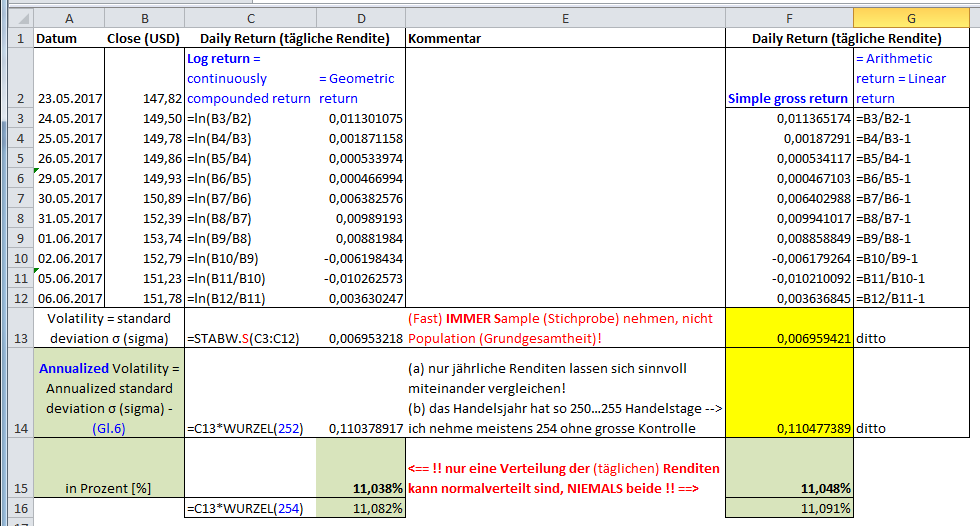
=> man sieht:
- es gibt bei der Annualisierten Volatilität bereits ein kleinen Unterschied
- man kann als Anlageberater seine publizierte Sharpe Ratio sehr leicht nach oben "tunen", indem man zum richtigen Rendite-Typ greift und/oder die Anzahl der Handelstage nach unten setzt!
=> so macht sich dieser kleine, aber feine Unterschied auf Sicht von mehreren Jahren bemerkbar (f):
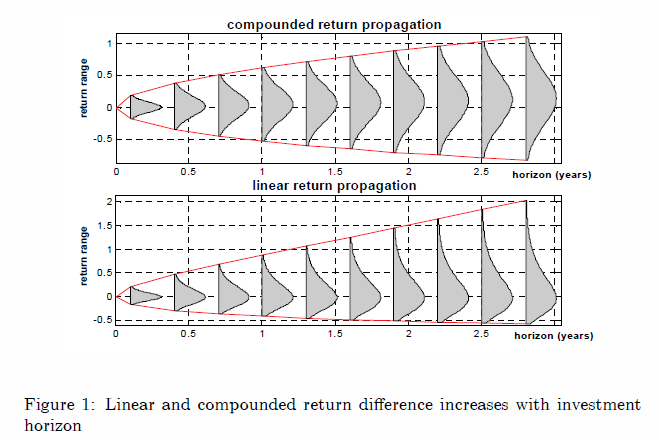
(siehe (e2) unten: oben sind die geometrischen Renditen normalverteilt, und damit unten die linearen Renditen log-normalverteilt, die ins Positive verzerrt sind )
__
Aus (e) ein paar Aussagen:
(e1) wenn geometrische Renditen normalverteilt sind, erhält man nie negative Preise; bei arithmetischen Renditen, die normalverteilt sind, ist das durchaus möglich und damit sinnlos (S.3).
(e2) wenn eine Variable X = log(Y) normalverteilt ist, dann ist Y log-normalverteilt (S.2).
(e3) das Produkt von normalverteilten Variablen ist nicht mehr normalverteilt (S.2).
=> das hat zur Folge, dass wenn ich annehme oder definiere meine täglichen Renditen sind normalverteil, dann sind meine daraus berechneten Wochen-, Monats-, und Jahresrenditen nicht mehr normalverteil und umgekehrt!
__
Also was nehmen, Log returns oder Simple returns?
=> ich würde immer noch sagen Log returns aus den 5 Gründen aus Beitrag Nr. 14, aber auch aus diesen Erwägungen:
- ursprünglich nahm Markowitz zu seiner Modern Portfolio Theory (MPT) normally distributed arithmetic returns an
- später, 1973, verwendeten Fischer Black und Myron S. Scholes bei der Black and Scholes formula for option pricing normally distributed geometric returns an, und zwar über alle Zeitebenen hinweg: https://de.wikipedia.org/wiki/Black-Scholes-Modell
- empirisch gesehen sollen lognormal distributions von Renditen sich den "wahren" Rendite-Verteilungen (die ja idR nicht normalverteilt sind --> "fat tails") ganz gut annähern --> (h)
- als nach Black und Scholes immer mehr evident wurde, dass Aktienkurse idR doch nicht so gut einen Random Walk hinlegen, geriet auch ihre Formel zunehmend unter Beschuss (und aus anderen Gründen). Wie immer, wurden dann weitere Adaptionen daran vorgenommen, um diesem Umstand im Zeitalter der Super-Quants Rechnung zu tragen. Allerdings hat sie halt bis heute Bestand, weil man mit ihr relativ einfach rechnen kann. Ich persönlich finde nicht, dass man eine Formel oder Model dadurch verwerfen sollte, nur weil es eine komplizierte Wirklichkeit nur "einigermassen gut" abbilden kann, statt perfekt. Und so sehe ich das eben auch mit den Log Returns. Da wo es Sinn macht sollte man sie bevorzugen, um effektiv weiterrechnen zu können. Man kann ja immer noch parallel mit Simple returns arbeiten, da wo angebracht.
__
Quellen:
(e) To log or not to log, The distribution of asset returns, Aas, 2004: https://www.nr.no/files/samba/bff/SAMBA0304.pdf
(f) Linear vs. Compounded Returns, Common Pitfalls in Portfolio Management, Meucci, 2010 --> siehe Beitrag Nr. 12 oben
(g) Geometric or Arithmetic Mean, A Reconsideration, Jacquier, Kane, Marcus, 2003: https://www2.bc.edu/alan-marcus/papers/FAJ_2003.pdf
(h) The Distribution of S&P 500 Index Returns, Egan, 2007: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=955639 --> Chartered Financial Analyst Program Curriculum, year 2006, level 1, volume 1, reading 10
Calculating returns (4) - Log returns für die Berechnung der Annualisierten Volatilität (2)
Zurück zum Problem der Berechnung der (historische) Standardabweichung aus einer Zeitreihe mit Renditen zu bestimmten, gleichdistanten Zeitpunkten.=> diese berechnete (=STABW.S(xx:yy)) Standardabweichung muss idR auf ein Jahr skaliert werden, um Vergleichbarkeit mit Zinssätzen etc. zu ermöglichen.
Da wir wie oben schon angedeutet unsere Log Returns als log-normal, also als normal verteilt annehmen (+), können wir - und nur dann - die Skalierung über diese Beziehung einfach vornehmen (aus (a) in Beitrag Nr. 13 --> ch.2.6 Volatility):
rt = ln(Pt) - ln(P(t-1)) ~ N(μ, σ^2) (Gl.7a)
mit N(μ, σ^2) als Normverteilung mit (wahrem) Mittelwert μ und (wahrer) Varianz = Standardabweichung^2 = σ^2.
Für h > 0, Anzahl der gleichdistanten Beobachtungen in einem Jahr, gilt dann entsprechend:
r(t+h) ~ N(μh, hσ^2) (Gl.7b)
Wenn wir also das erste Formelergebnis zur Standardabweichung σ0 mit dem Faktor √(h) (Wurzel von h) gewichten, bekommen wir die Annualisierte Volatilität:
σann = √(h)σ0 (Gl.8)
Also, bei:
- täglichen Log returns nehmen wir h = 250...255 (ich nehme immer unbesehen 254 - die Anzahl der Handelstage pro Jahr ist weltweit unterschiedlich und am selben Markt durch sich verschiebende Feiertage auch nicht immer konstant über die Jahre hinweg)
- wöchentlichen Log returns nehmen wir h = 52, und bei
- monatlichen Log returns nehmen wir h = 12.
__
Hier ist ein Beispiel dazu aus: http://www.investopedia.com/ask/answers/021015/how-can-you-c…
=>

A priori halte ich an dieser Stelle fest:
1. die täglichen Renditen sind hier arithmetisch, nicht logarithmisch. Die arithmetischen Renditen können durchaus als normalverteilt angenommen werden, um zu einem besseren Ergebnis bzgl. der Annualisierten Volatilität zu kommen.
2. diese Annahme ist aber nur implizit durch mich gemacht worden, nicht durch den Autor. Damit kann dieses Beispiel auf einer nicht beabsichtigten Annahme beruhen und damit das Ergebnis verfälschen (bei kleinen Zeiträumen spielt so eine Ergebnis-Verfälschung noch keine grosse Rolle, aber bei Berechnungen über mehrere Jahre hinweg, v.a. bei möglicher zunehmender Volatilität und Abnahme der zeitlichen Aüflösung, also von Tag zu Woche zu Monat usw. --> (e), (f) )
Daher zur Veranschaulichung mein Nachbau mit den arithmetischen (simplen, linearen) Tagesrenditen (rechts) und meinen logarithmischen (geometrischen) Renditen (links):

=> man sieht:
- es gibt bei der Annualisierten Volatilität bereits ein kleinen Unterschied
- man kann als Anlageberater seine publizierte Sharpe Ratio sehr leicht nach oben "tunen", indem man zum richtigen Rendite-Typ greift und/oder die Anzahl der Handelstage nach unten setzt!
=> so macht sich dieser kleine, aber feine Unterschied auf Sicht von mehreren Jahren bemerkbar (f):

(siehe (e2) unten: oben sind die geometrischen Renditen normalverteilt, und damit unten die linearen Renditen log-normalverteilt, die ins Positive verzerrt sind )
__
Aus (e) ein paar Aussagen:
(e1) wenn geometrische Renditen normalverteilt sind, erhält man nie negative Preise; bei arithmetischen Renditen, die normalverteilt sind, ist das durchaus möglich und damit sinnlos (S.3).
(e2) wenn eine Variable X = log(Y) normalverteilt ist, dann ist Y log-normalverteilt (S.2).
(e3) das Produkt von normalverteilten Variablen ist nicht mehr normalverteilt (S.2).
=> das hat zur Folge, dass wenn ich annehme oder definiere meine täglichen Renditen sind normalverteil, dann sind meine daraus berechneten Wochen-, Monats-, und Jahresrenditen nicht mehr normalverteil und umgekehrt!
__
Also was nehmen, Log returns oder Simple returns?
=> ich würde immer noch sagen Log returns aus den 5 Gründen aus Beitrag Nr. 14, aber auch aus diesen Erwägungen:
- ursprünglich nahm Markowitz zu seiner Modern Portfolio Theory (MPT) normally distributed arithmetic returns an
- später, 1973, verwendeten Fischer Black und Myron S. Scholes bei der Black and Scholes formula for option pricing normally distributed geometric returns an, und zwar über alle Zeitebenen hinweg: https://de.wikipedia.org/wiki/Black-Scholes-Modell
- empirisch gesehen sollen lognormal distributions von Renditen sich den "wahren" Rendite-Verteilungen (die ja idR nicht normalverteilt sind --> "fat tails") ganz gut annähern --> (h)
- als nach Black und Scholes immer mehr evident wurde, dass Aktienkurse idR doch nicht so gut einen Random Walk hinlegen, geriet auch ihre Formel zunehmend unter Beschuss (und aus anderen Gründen). Wie immer, wurden dann weitere Adaptionen daran vorgenommen, um diesem Umstand im Zeitalter der Super-Quants Rechnung zu tragen. Allerdings hat sie halt bis heute Bestand, weil man mit ihr relativ einfach rechnen kann. Ich persönlich finde nicht, dass man eine Formel oder Model dadurch verwerfen sollte, nur weil es eine komplizierte Wirklichkeit nur "einigermassen gut" abbilden kann, statt perfekt. Und so sehe ich das eben auch mit den Log Returns. Da wo es Sinn macht sollte man sie bevorzugen, um effektiv weiterrechnen zu können. Man kann ja immer noch parallel mit Simple returns arbeiten, da wo angebracht.
__
Quellen:
(e) To log or not to log, The distribution of asset returns, Aas, 2004: https://www.nr.no/files/samba/bff/SAMBA0304.pdf
(f) Linear vs. Compounded Returns, Common Pitfalls in Portfolio Management, Meucci, 2010 --> siehe Beitrag Nr. 12 oben
(g) Geometric or Arithmetic Mean, A Reconsideration, Jacquier, Kane, Marcus, 2003: https://www2.bc.edu/alan-marcus/papers/FAJ_2003.pdf
(h) The Distribution of S&P 500 Index Returns, Egan, 2007: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=955639 --> Chartered Financial Analyst Program Curriculum, year 2006, level 1, volume 1, reading 10
Antwort auf Beitrag Nr.: 55.476.543 von faultcode am 08.08.17 00:17:18
Dazu muss man die (historische) Volatilität wissen, also die (historische) Standardabweichung.
Hierbei ist es nicht damit getan in Excel einfach =STABW.S(xx:yy) über eine Zeitreihe mit Renditen zu bestimmten Zeitpunkten als Formel zu verwenden.
Dazu Folgendes:
(a) idR verwendet man im Börsengeschehen immer nur Sample (Stichprobe) und nicht Population (Grundgesamtheit) (weil wir die oft oder meistens nicht kennen), auch wenn bei grossem Sample-Umfang sich beide Grössen annähern:
Population standard deviation:
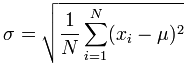
Sample standard deviation:
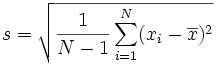
Hier gibt es gute Formeln zum Berechnen der Standardabweichung bei gerade laufenden Zeitreihen - also für eine Echtzeitberechnung: https://www.johndcook.com/blog/standard_deviation/
So macht sich die Verwendung von =STABW.S(xx:yy) im Gegensatz zu =STABW.N(xx:yy) bei den letzten drei DAX30-Jahren (Performance, nur Schlusskurse) bemerkbar:
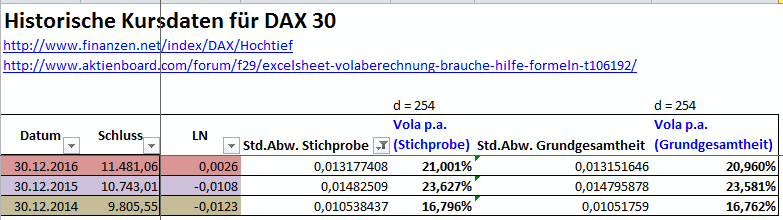
..und selbst diese geschätzten Volatilitäten können noch verbessert werden, wenn man auch die Intraday-Volatilität beim DAX30 berücksichtigen würde.
Dazu hat Parkinson (1980) eine tägliche High and Low-Formel entwickelt: http://www.ivolatility.com/help/3.html
..und Garman and Klass (1980) eine Formel, die auch noch das tägliche Open, High, Low und Close berücksichtigt: https://quant.stackexchange.com/questions/11306/what-is-the-…
(--> Range-based volatility estimates)
=> nun sollte klar sein, warum Stichprobe beim Börsengeschehen idR vorzuziehen ist, und warum Vola-Angaben immer mit Vorsicht zu geniessen sind.
=> es ist daher ein bischen gefährlich, Vola-Angaben aus verschiedenen Quellen zu vergleichen, wenn nicht klar ist, wie die Berechnungen im Detail zustande gekommen sind.
Ich lese sie daher eher relativ zueinander innerhalb einer Veröffentlichung.
Calculating returns (4) - Log returns für die Berechnung der Annualisierten Volatilität (1)
Nachdem nun ein paar Grundlagen geklärt sind, hier nun die Berechnung auf die der derzeitige Gedankenfluss gerichtet ist, nämlich eine sachgerechte Berechnung der (historischen) Sharpe ratio.Dazu muss man die (historische) Volatilität wissen, also die (historische) Standardabweichung.
Hierbei ist es nicht damit getan in Excel einfach =STABW.S(xx:yy) über eine Zeitreihe mit Renditen zu bestimmten Zeitpunkten als Formel zu verwenden.
Dazu Folgendes:
(a) idR verwendet man im Börsengeschehen immer nur Sample (Stichprobe) und nicht Population (Grundgesamtheit) (weil wir die oft oder meistens nicht kennen), auch wenn bei grossem Sample-Umfang sich beide Grössen annähern:
Population standard deviation:
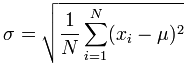
Sample standard deviation:
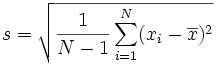
Hier gibt es gute Formeln zum Berechnen der Standardabweichung bei gerade laufenden Zeitreihen - also für eine Echtzeitberechnung: https://www.johndcook.com/blog/standard_deviation/
So macht sich die Verwendung von =STABW.S(xx:yy) im Gegensatz zu =STABW.N(xx:yy) bei den letzten drei DAX30-Jahren (Performance, nur Schlusskurse) bemerkbar:

..und selbst diese geschätzten Volatilitäten können noch verbessert werden, wenn man auch die Intraday-Volatilität beim DAX30 berücksichtigen würde.
Dazu hat Parkinson (1980) eine tägliche High and Low-Formel entwickelt: http://www.ivolatility.com/help/3.html
..und Garman and Klass (1980) eine Formel, die auch noch das tägliche Open, High, Low und Close berücksichtigt: https://quant.stackexchange.com/questions/11306/what-is-the-…
(--> Range-based volatility estimates)
=> nun sollte klar sein, warum Stichprobe beim Börsengeschehen idR vorzuziehen ist, und warum Vola-Angaben immer mit Vorsicht zu geniessen sind.
=> es ist daher ein bischen gefährlich, Vola-Angaben aus verschiedenen Quellen zu vergleichen, wenn nicht klar ist, wie die Berechnungen im Detail zustande gekommen sind.
Ich lese sie daher eher relativ zueinander innerhalb einer Veröffentlichung.
22:19 Uhr · dpa-AFX · Dow Jones |
20:11 Uhr · dpa-AFX · 3M |
19:19 Uhr · Markus Fugmann · DAXAnzeige |
16:52 Uhr · dpa-AFX · 3M |
15:48 Uhr · dpa-AFX · Dow Jones |
15:20 Uhr · BNP Paribas · Dow JonesAnzeige |
15:07 Uhr · SG Zertifikate · S&P 500Anzeige |
14:05 Uhr · dpa-AFX · 3M |
10:07 Uhr · Markus Fugmann · DAXAnzeige |
07:36 Uhr · wallstreetONLINE Redaktion · S&P 500 |
| Zeit | Titel |
|---|---|
| 09.05.24 | |
| 06.05.24 | |
| 23.04.24 | |
| 21.04.24 | |
| 26.03.24 | |
| 14.03.24 | |
| 22.02.24 | |
| 13.02.24 | |
| 13.02.24 | |
| 30.01.24 |





















